神奈川県の公立高校入試で数学はかなりやっかいな科目です。思考力や応用力を問う出題が増加傾向にあります。単なる公式暗記では太刀打ちできない内容も多くなっています。
この記事では、
- 平均点や得点分布からわかること
- 大問ごとの出題傾向
- 効果的な学習法と今後の対策ポイント
を解説していきます。
公立高校入試(数学)の特徴
難易度の変化と平均点の推移
数学の平均点の推移はこんな感じです。
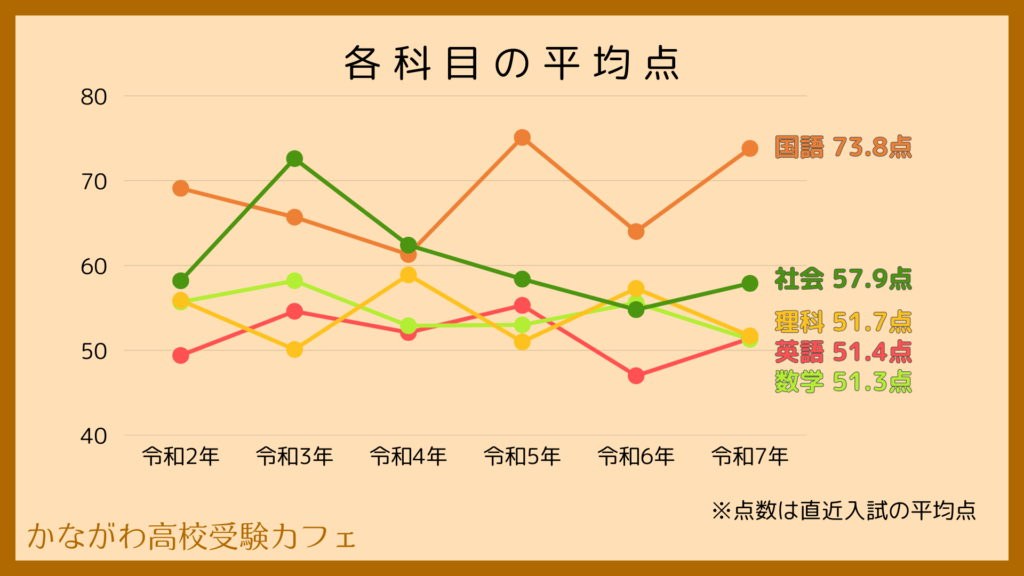
数学の平均点は5科目の中では低く難易度は比較的高めです。令和7年入試ではもっとも平均点が低い科目となりました。また、5科目の中で変動がもっとも小さいのが特徴です。今後は50点を割り込むことは考えられますが、他の科目が大幅に難化しない限りは60点を超えることは無いと考えられます。
得点分布から読み取れる傾向
令和7年度の数学の得点分布はこんな感じです。
多くの受験生が50〜60点台に集中していることが分かります。基本的な計算処理やシンプルな単問もあるため、50点までは比較的とりやすい出題が続いています。数学が苦手な人にとってはある程度の得点源にできます。一方、80点台から急激に数が減っています。数学の特徴として「正答率が1ケタ台の問題が例年出題される」，「高難易度の問題の配点が6点と大きい」というものがあります。このことから、上位ほどまわりと差がつけにくい傾向が続いています。
各大問ごとの特徴と攻略法
例年の大問構成とその特徴です。
| 大問 | 内容 | 配点 | 特徴と対策 |
| 問1 | 計算問題 | 15点 | 基本的な計算力を問う。確実に取りたい。 |
| 問2 | 小問集合 | 24点 | 各分野からの基礎・標準問題。計算の正確さが鍵。 |
| 問3 | 応用問題 | 26点 | 多ステップの問題や証明を含む。思考の柔軟性が重要。 |
| 問4 | 関数 | 15点 | グラフ・変化の割合・関係式を絡めた出題。実験的要素も。 |
| 問5 | 確率 | 10点 | 場合分けと論理的思考が必須。条件付き確率にも注意。 |
| 問6 | 空間図形 | 10点 | 投影図・体積・展開図など。空間認識力が必要。 |
問1【基本計算問題】
正負の数・文字式・方程式などの基本計算。スピードと正確性が問われます。ミスを防ぐためにも、計算手順を省略せず丁寧に書く習慣が大切です。県内正答率も90%近くあり，問2以降の解答の前提能力ともなるため、全問正解をして確実に得点したい問題です。
問2【小問集合】
関数・資料の整理・図形などから基礎〜標準レベルの小問が出題されます。分野横断的な知識と、状況に応じたアプローチ力が求められますが、問3以降と比べると。入試対策用のテキストなどにも掲載されているレベルで、正答率も高い問題です。
問3【応用・文章題】
設問4問で構成されています。出題順はまちまちですが，『図形の証明問題(選択式)＋計量問題』，『データの活用』，『平面図形の計量問題』，『速さ・割合の文章題』で構成されることが多いです。近年は論理的思考力を問う設定が多く、正答率も低い傾向が続いています。特に『平面図形の計量問題』は高難易度問題の1つであり，例年の正答率は1桁台です。問題へのアプローチも年によって異なるため，対策がしにくい問題の筆頭です。
問4【関数】
座標の導出や関数の式，図形の性質への活用力が問われます。傾向はここ数年変わっておらず，(ア)は関数の式を求める問題，(イ)は直線の式を求める問題，(ウ)は応用となっています。
(イ)までは解き方もワンパターンであり，座標が求められれば解答までに時間を必要としないため得点源となる問題です。
(ウ)は高難易度問題の1つです。答えにたどりつくまでに計算処理の量が多いため，計算ミスや解答時間不足が起こりやすい問題です。時間配分や問題を解く順番をしっかり考えて入試に臨みましょう。
問5【確率】
さいころを2個投げて条件にあてはまるパターンを求める問題が続いています。地道に調べれば答えにたどり着くことができます。一方で「かなりの時間を要する」「検証が難しい」といった難点もある問題です。
問6【空間図形】
立体図形の体積、展開図、投影図など、空間把握力が問われます。図を描く力と、立体を頭の中でイメージする力が必要です。空間図形は平面をくりぬき、平面図形の問題として扱うのが定番です。空間認識と平面図形の知識，パターンが要求されます。
入試に求められる力
神奈川県の数学入試で求められる力は以下の通りです。
- 計算力：正確でスピーディな処理能力
- 思考力・論理力：複数条件を整理し、解法を構築する力
- 図形認識力：空間図形や平面図形の把握と処理能力
- 応用力：関数や確率など、知識を新しい場面で活用する力
数学という科目の特性として「暗記がほぼ無い」というのがあります。その分、原理・原則をおさえ活用することが求められます。
効果的な学習法と対策
いきなりの過去問は危険！
数学はかなりの難易度があります。入試用テキストや早い時期の模試の再演習などで、基本的な問題を解けるようにしてから過去問に臨むと良いでしょう。
過去問演習の活用
本番と同形式の問題に慣れ、出題パターンを把握しておきましょう。特に高難易度の問題は初見でスムーズに解ける問題の方が少ないです。過去問を通して「解き方の型」を知っておくと対応できる問題が広がっていくでしょう。
時間配分の戦略
高難易度問題の影響もあり50分で「全問題完璧！」となる受験生は少ないでしょう。「この問題は捨てる」など、自分なりの時間配分の戦略を持っておくことが大事です。
まとめ｜今後の展望
数学は少しずつ平均点が低下しています。若干の出題方法の変化はありましたが、平均点の低下傾向は続いています。今後の入試でもこの傾向は継続すると予想されます。一方で大きな出題傾向の変更が無いことから、前もって時間配分などの対策がとれる科目です。過去問の徹底活用と苦手分野の着実な克服を通じて、着実に得点力を伸ばしていきましょう。
